5 Introduction to Statistics in R

install.packages("ggplot2",  repos = "https://cran.us.r-project.org")
install.packages("dplyr",  repos = "https://cran.us.r-project.org")
install.packages("ggfortify",  repos = "https://cran.us.r-project.org")

library(ggplot2)
library(dplyr)
library(ggfortify)

urlfile05a="https://raw.githubusercontent.com/apicellap/data/main/ladybirds_morph_colour.csv"
lady<-read.csv(url(urlfile05a))
head(lady)

##   Habitat Site morph_colour number
## 1   Rural   R1        black     10
## 2   Rural   R2        black      3
## 3   Rural   R3        black      4
## 4   Rural   R4        black      7
## 5   Rural   R5        black      6
## 6   Rural   R1          red     15

View data structure:

str(lady)

## 'data.frame':    20 obs. of  4 variables:
##  $ Habitat     : chr  "Rural" "Rural" "Rural" "Rural" ...
##  $ Site        : chr  "R1" "R2" "R3" "R4" ...
##  $ morph_colour: chr  "black" "black" "black" "black" ...
##  $ number      : int  10 3 4 7 6 15 18 9 12 16 ...

5.1 $\chi$$^{2}$ contingency table analysis

Create new dataframe, totals:

totals <- lady %>% #working with this dataframe
  group_by(Habitat, morph_colour) %>% #we want to represent these groups in the dataframe
  summarise(total.number = sum(number)) #add up the numbers of each group using the new object total.number

## `summarise()` has grouped output by 'Habitat'. You can override using the
## `.groups` argument.

totals

## # A tibble: 4 × 3
## # Groups:   Habitat [2]
##   Habitat    morph_colour total.number
##   <chr>      <chr>               <int>
## 1 Industrial black                 115
## 2 Industrial red                    85
## 3 Rural      black                  30
## 4 Rural      red                    70

Create bar chart:

base_plot<-ggplot(totals, aes(x=Habitat, y=total.number,
                  fill = morph_colour)) + #fill is used when there is something like a bar that can be filled with color 
                                          #if this were color = morph_colour, then the argument would affect the bar's outline
  geom_bar(
    stat = 'identity', #this tells ggplot not to calculate anything from the data and just display the data as they are in the dataframe
    position = 'dodge' #this is request to put the two bars in each Habitat group next to each other 
                       #if it's not used, a stacked barplot would be printed 
  ) 
base_plot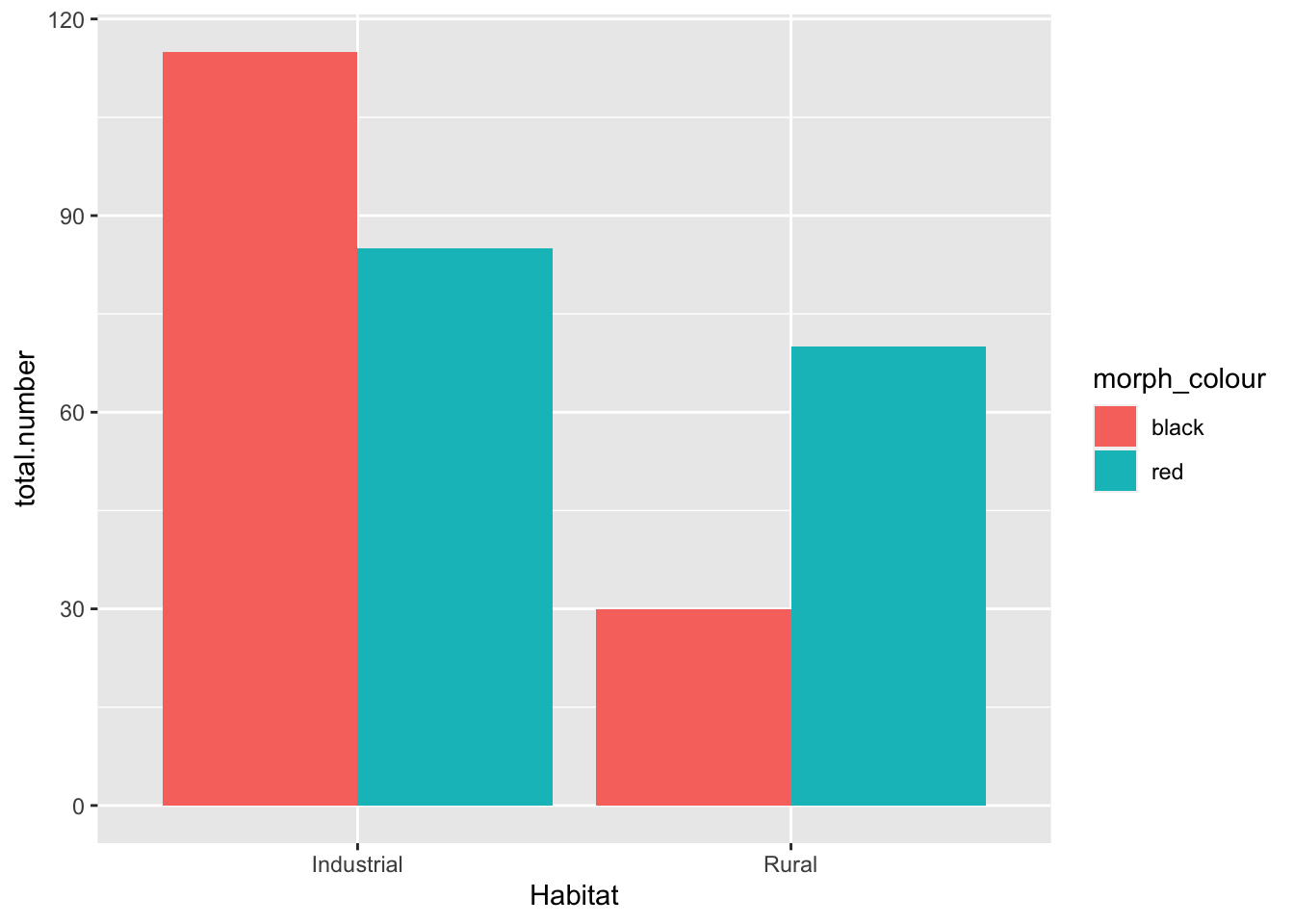

base_plot +   
  scale_fill_manual(values = c(black = "black", red = "red")) #the text in "" are the colors we are instructing R to fill the bars with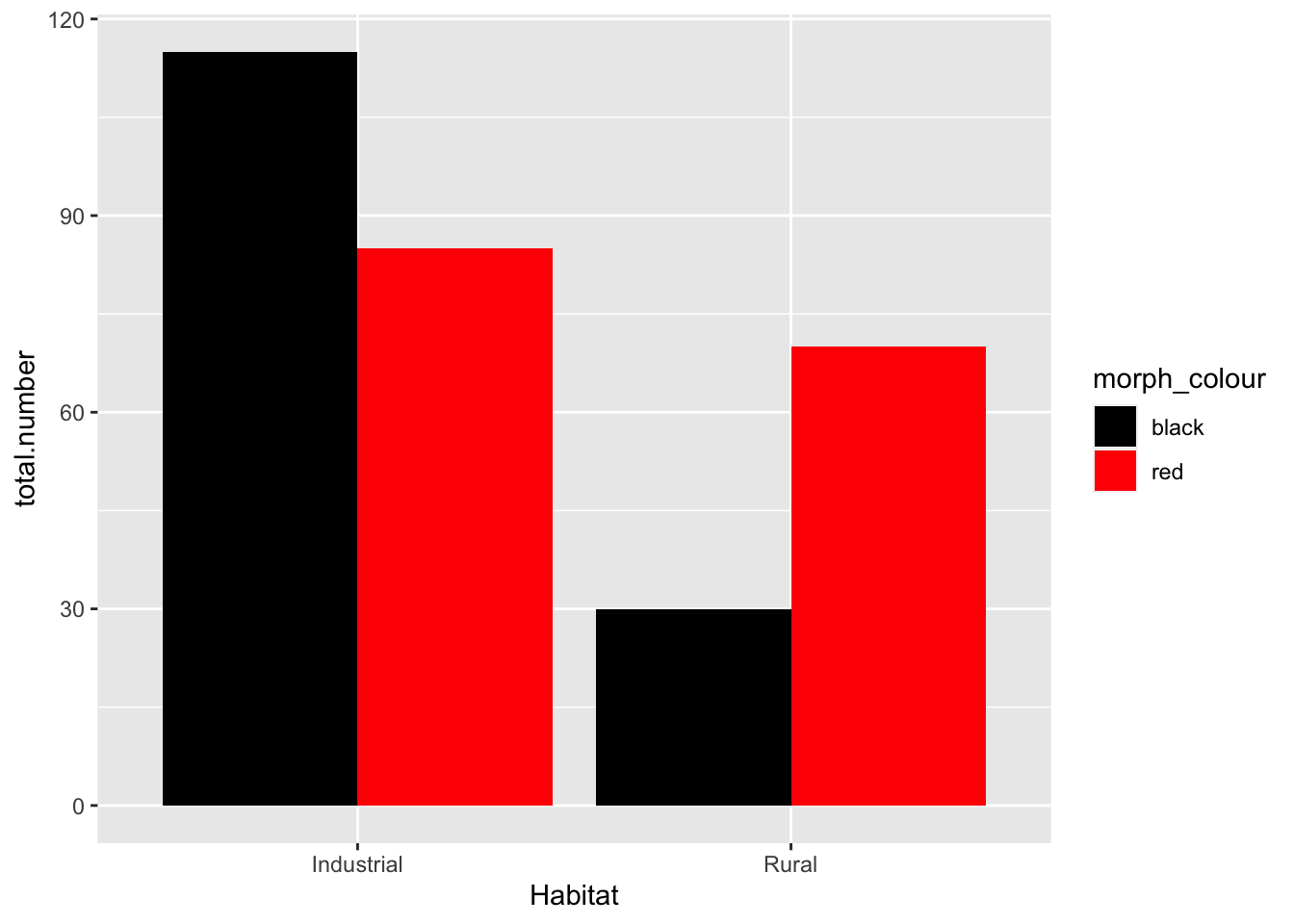

Null hypothesis: there is no association between the color of the birds and their habitat
- My opinion: data suggest that there is a higher proportion of colored birds in the industrial habitat. We should reject the null hypothesis (pre-stats)
- to rigorously test this, a chi-squared test must be performed

5.2 Making the $\chi$$^{2}$ Test

Use xtabs() function to generate a contingency table:

lady.mat <-xtabs(                     #function converts dataframe into a matrix, which is different from a dataframe
                  number ~ Habitat + morph_colour, #cross-tabulate the number of column counts in the dataframe by the Habitat and morph_colour variables
                 data = lady) 
lady.mat

##             morph_colour
## Habitat      black red
##   Industrial   115  85
##   Rural         30  70

Perform a $\chi$$^{2}$ test on the matrix:

lady.chi<-chisq.test(lady.mat) #chi squared test function performed on matrix 
lady.chi

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  lady.mat
## X-squared = 19.103, df = 1, p-value = 1.239e-05

the p value is 0.00001239 - this is the probability that the pattern arose by chance.
- It is lower than 0.05, so we can reject the null hypothesis

names(lady.chi) #can examine all of the parts of the test mechanics

## [1] "statistic" "parameter" "p.value"   "method"    "data.name" "observed" 
## [7] "expected"  "residuals" "stdres"

5.3 Two-sample t-test

The two-sample t-test compares the means of two groups of numeric values
It is appropriate when the sample sizes of these two groups is small
The analysis makes the following assumptions about the data:
- The data are normally distributed
- The variances of the data are equivalent

urlfile05b="https://raw.githubusercontent.com/apicellap/data/main/ozone.csv"
ozone<-read.csv(url(urlfile05b))
glimpse(ozone)

## Rows: 20
## Columns: 3
## $ Ozone           <dbl> 61.7, 64.0, 72.4, 56.8, 52.4, 44.8, 70.4, 67.6, 68.8, …
## $ Garden.location <chr> "West", "West", "West", "West", "West", "West", "West"…
## $ Garden.ID       <chr> "G1", "G2", "G3", "G4", "G5", "G6", "G7", "G8", "G9", …

5.3.1 The first step: Plot your data

Create histograms of the data, by Garden.location variable:

ggplot(ozone, aes(x=Ozone))+ #since this is a histogram, x must be a continuous variable; cannot be categorical 
  geom_histogram(binwidth=10) + 
  facet_wrap(~Garden.location, #Divide data up into groups by this variable 
            ncol=1 ) +  #stacks the graphs on top of each other - 1 column 
  theme_bw()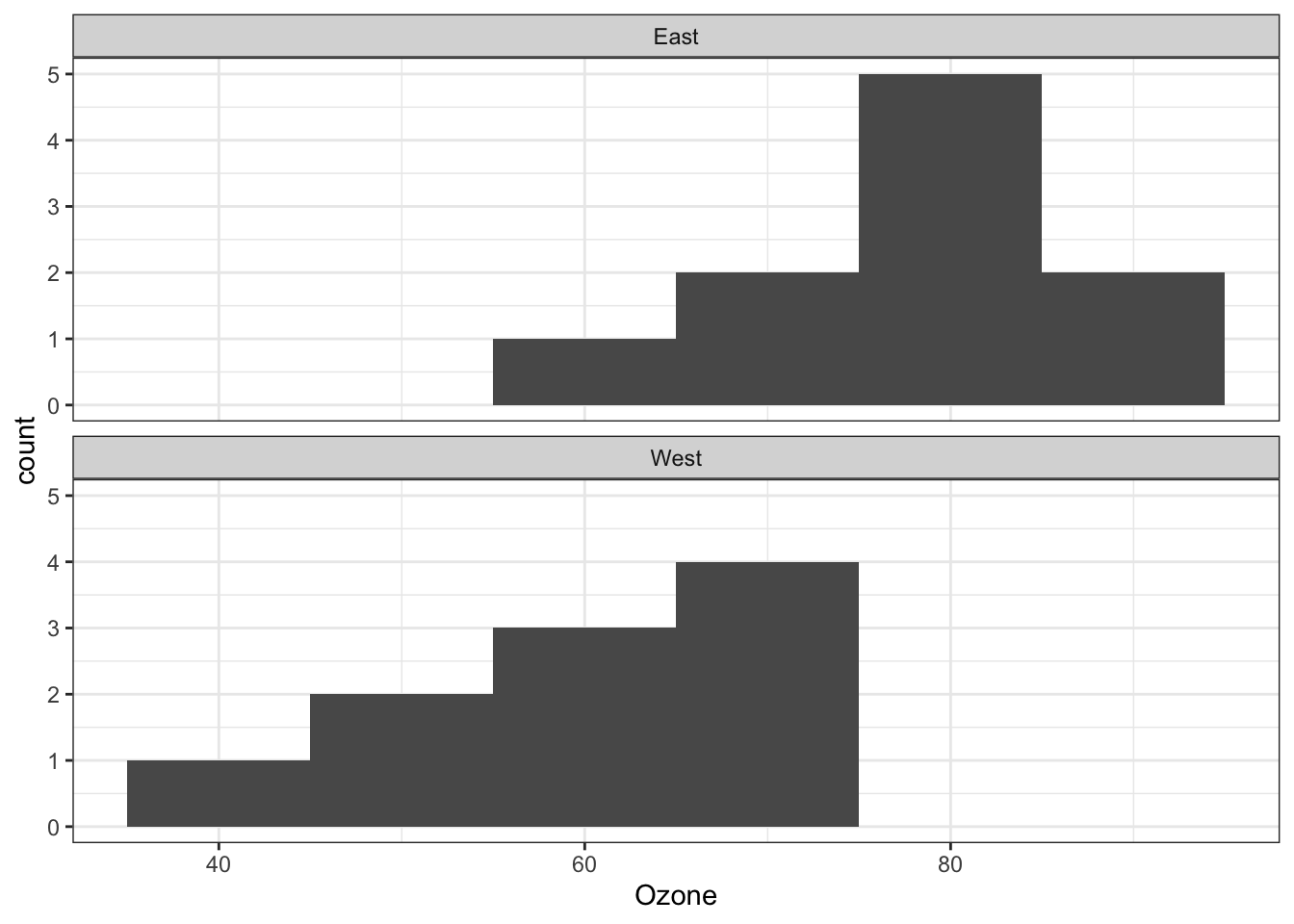

graph shows that assumptions of normality and equality of variance are met
- R has functions to evaluate these aspects more rigorously too

Count the number of observations when variable is ‘East’:

x<-sum(with(ozone, Garden.location == "East")) 
x

## [1] 10

summary<-ozone %>% 
  group_by(Garden.location) %>% 
  summarise(mean = mean(Ozone), SE = (sd(Ozone))/sqrt(x))
summary

## # A tibble: 2 × 3
##   Garden.location  mean    SE
##   <chr>           <dbl> <dbl>
## 1 East             77.3  2.49
## 2 West             61.3  2.87

Plot the ozone data as a barplot:

OzBrP<-ggplot(summary, aes(x = Garden.location, y = mean)) + #x defined as grazing treatment, y as fruit production
  geom_col() + 
  geom_errorbar(aes(x=Garden.location, ymin=mean -SE, ymax=mean*1+SE, width=.2),
                                            position = 'dodge')
OzBrP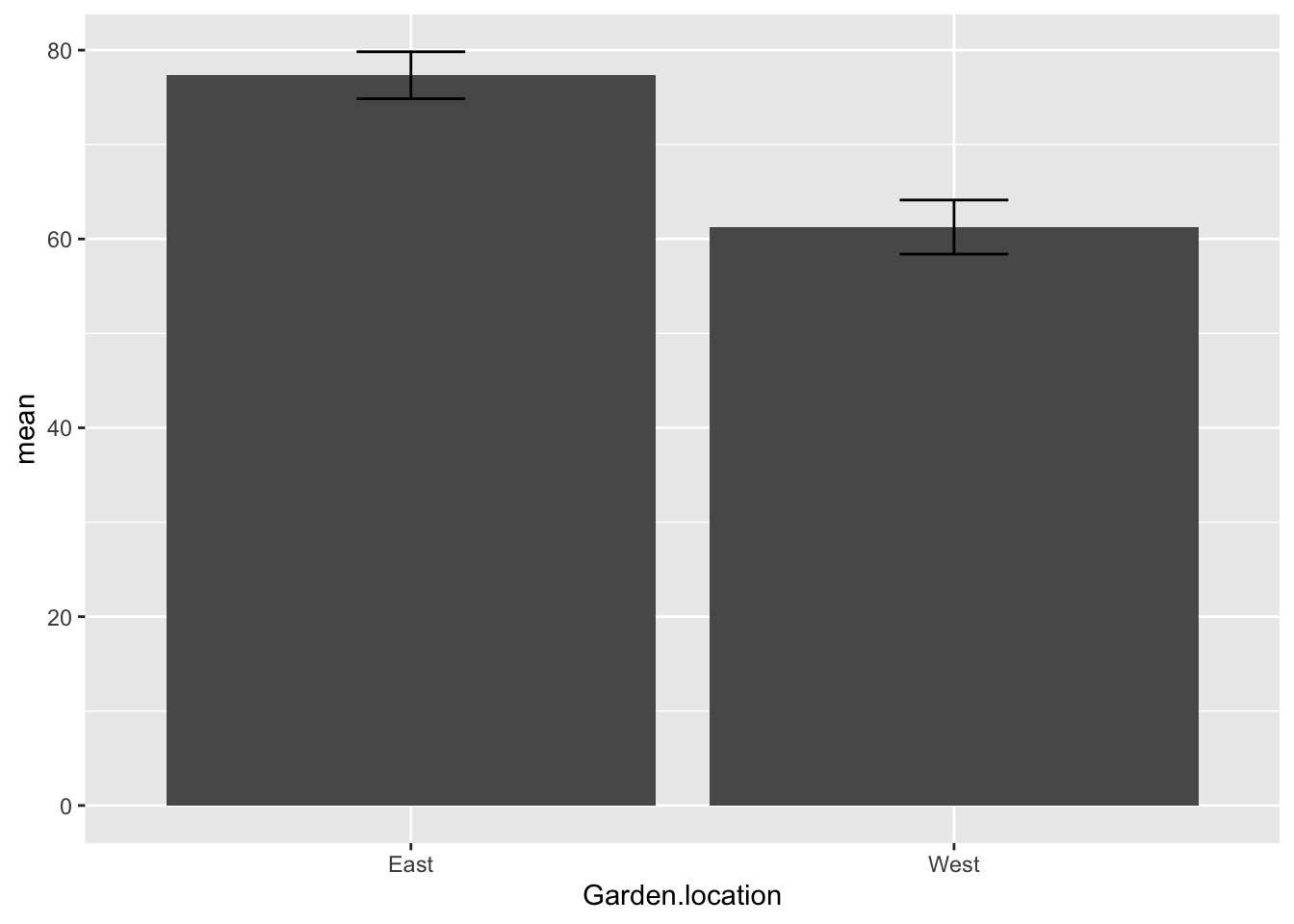

Plot the ozone data as a boxplot:

OzBxP <-ggplot(ozone, aes(x = Garden.location, y = Ozone)) + 
  geom_boxplot()
OzBxP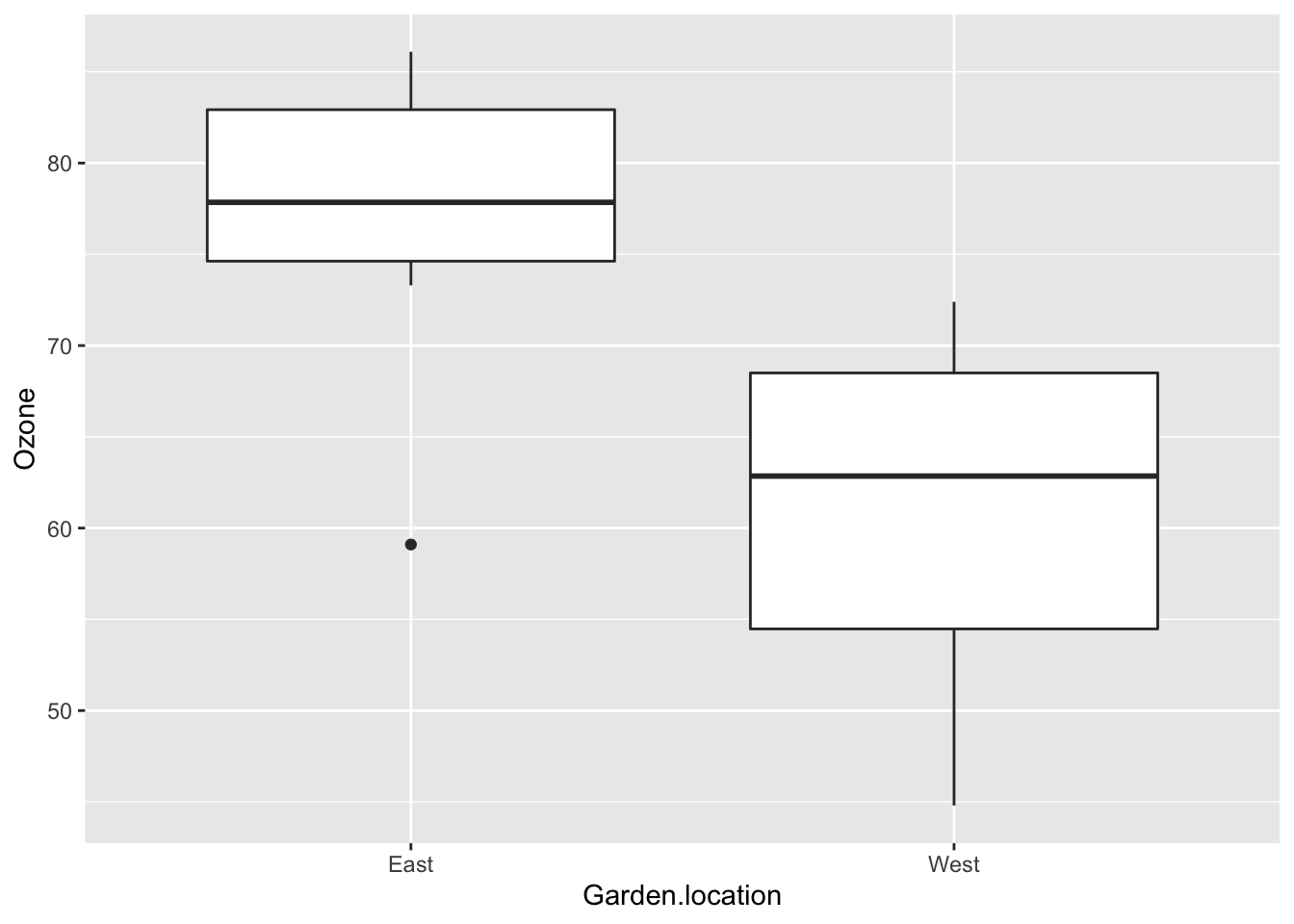

null hypothesis: there is no difference in ozone levels between the East and West garden locations
my opinion based on the boxplot - reject the null hypothesis

5.3.2 Two sample t-test analysis

Perform two sample t-test on the ozone dataset:

t.test(Ozone ~ Garden.location, #expression means do ozone levels vary as a function of location? That's how the ~ reads 
       data = ozone)

## 
##  Welch Two Sample t-test
## 
## data:  Ozone by Garden.location
## t = 4.2363, df = 17.656, p-value = 0.0005159
## alternative hypothesis: true difference in means between group East and group West is not equal to 0
## 95 percent confidence interval:
##   8.094171 24.065829
## sample estimates:
## mean in group East mean in group West 
##              77.34              61.26

the default of this two sample t-test is the Welch’s version
- In Welch version, the assumption about equal variance is relaxed and allows that you do not have to test for equal variance
The GSwR authors suggest not testing for equal variance
note regarding the Confidence interval (CI): the line about the 95% CI is 8.1-24.1. Since this range does not include 0 says that the means are statistically different from each other. This is congruent with the p value of the t-test

5.4 Linear models

Linear models are a class of analyses that include regression, multiple regression, ANOVA, and ANCOVA
- they are centered around a similiar framework of ideas such as a common set of assumptions about the data like the idea that the data are normally distributed

5.5 Simple linear regression

This section focuses on a dataset that compares plant growth rates to soil moisture content
The response (dependent) variable is that of plant growth rate
Plant growth rate is plotted against the explanatory (independent) variable, soil moisture content
- This variable is a continuous, numeric variable which does not have categories

Read and view structure of the data:

urlfile05c="https://raw.githubusercontent.com/apicellap/data/main/plant.growth.rate.csv"
plant_gr<-read.csv(url(urlfile05c))
glimpse(plant_gr) #two continuous (numeric) variables. they have no categories

## Rows: 50
## Columns: 2
## $ soil.moisture.content <dbl> 0.4696876, 0.5413106, 1.6979915, 0.8255799, 0.85…
## $ plant.growth.rate     <dbl> 21.31695, 27.03072, 38.98937, 30.19529, 37.06547…

5.5.1 Getting and plotting the data

Plot the plant growth (pg) data:

ggplot(plant_gr,
       aes(x=soil.moisture.content, y=plant.growth.rate)) +
  geom_point()+ 
  ylab("Plant Growth Rate (mm/week)") + 
  theme_bw()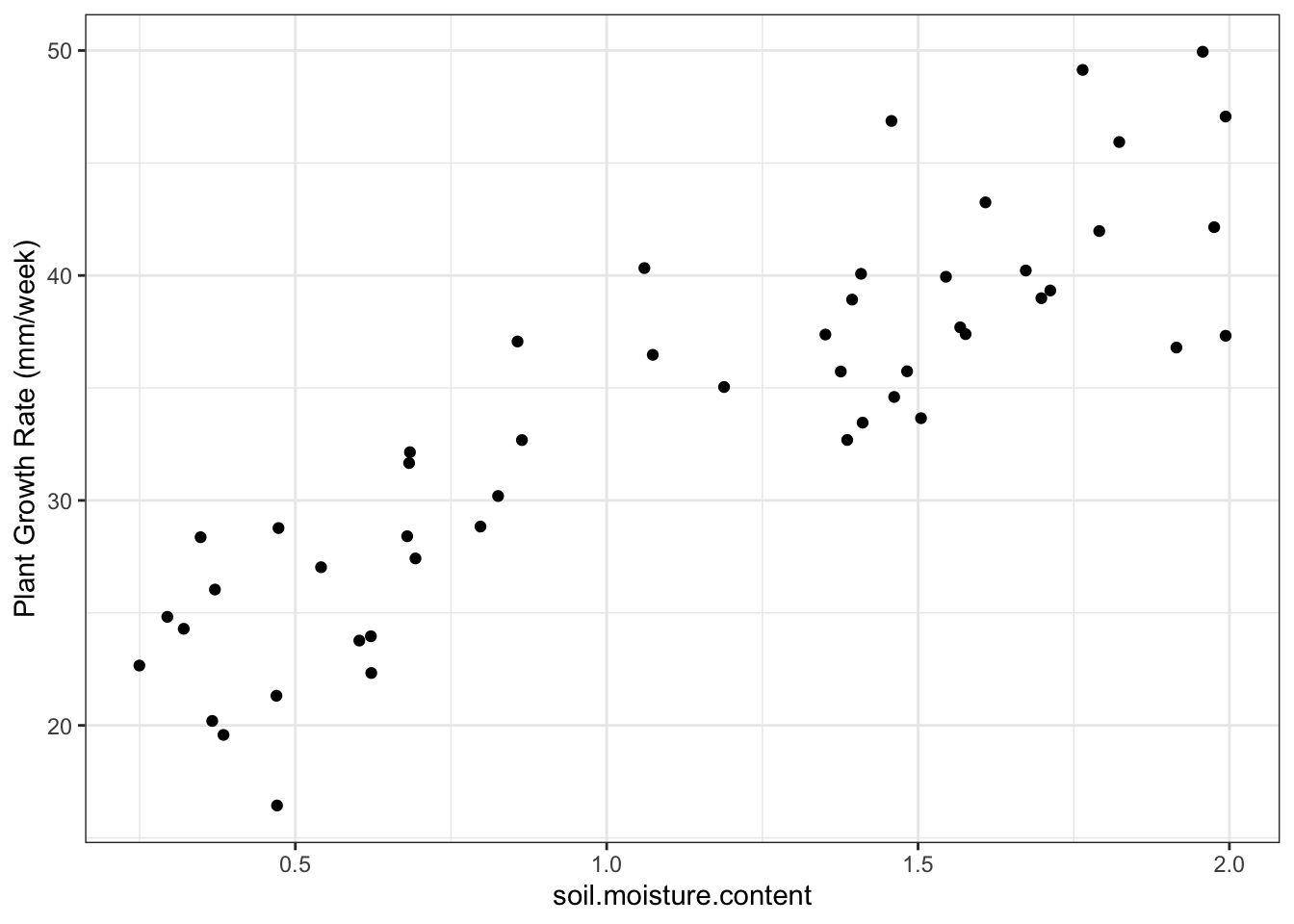

Plot shows that there is a probably a positive linear relationship between the two variables
- There is a slope of about 15 mm/week
- preliminary analysis: probably will reject the null hypothesis that soil moisture does not affect plant growth

5.5.2 Making a simple linear regression happen

Create a linear model:

model_pgr <- lm(plant.growth.rate ~ soil.moisture.content, data = plant_gr) #plant growth rate is a function of soil moisture content
model_pgr

## 
## Call:
## lm(formula = plant.growth.rate ~ soil.moisture.content, data = plant_gr)
## 
## Coefficients:
##           (Intercept)  soil.moisture.content  
##                 19.35                  12.75

5.5.3 Assumptions first

Check assumptions with ggfortify:

autoplot(model_pgr, 
         smooth.colour = NA)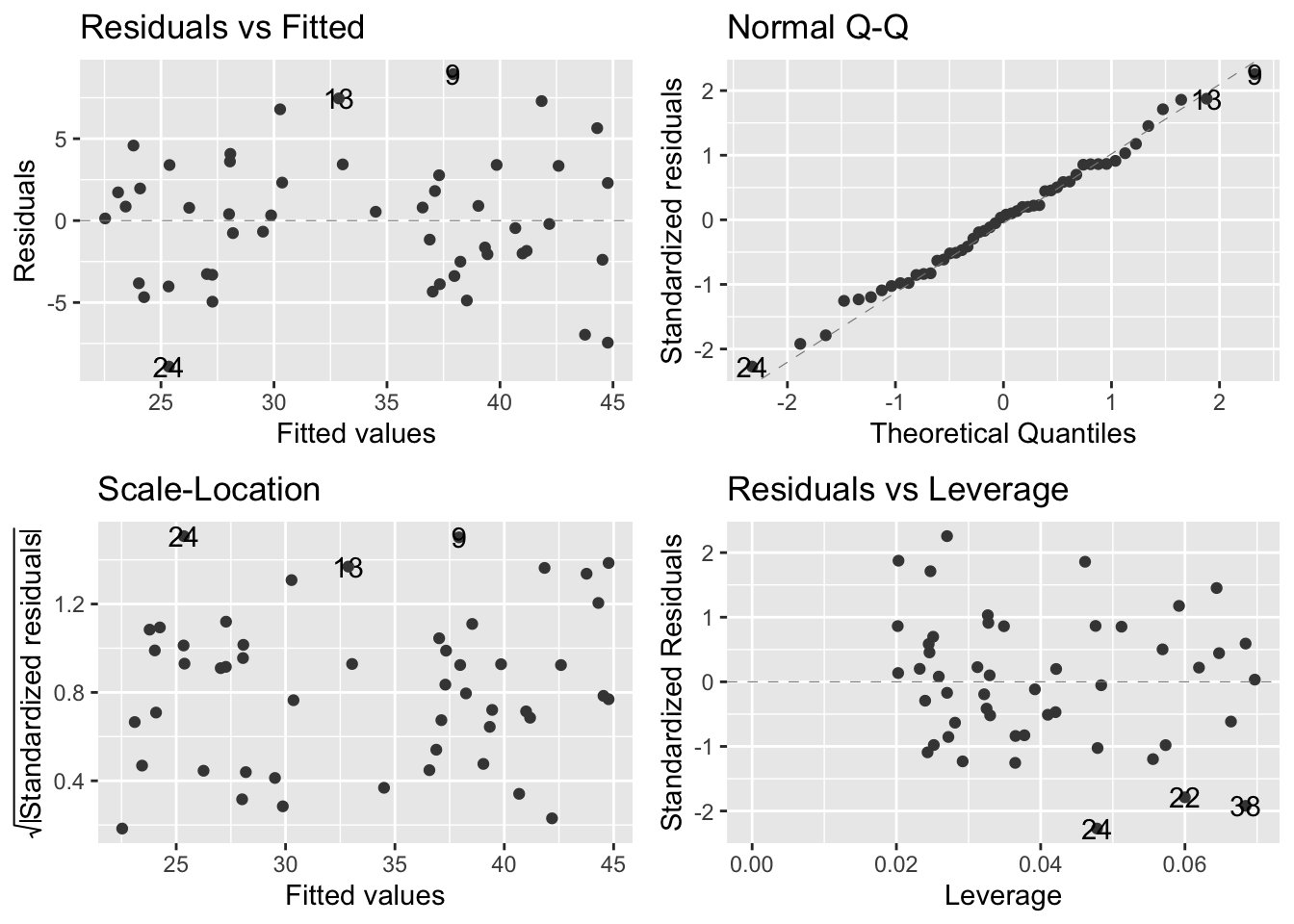

ggfortify plots:
- Top left - informs us on whether the line is an appropriate fit to the data; flat line means model is a good fit. Humps/valleys -> poor fit
- Top right - dots = residuals; dashes line = expectation under normal distribution. Better tool than histogram to assess normal distribution
- Bottom left - evaluates assumption of equal variance. linear models assume that variance is constant over all predicted values of the response variable. There should be no pattern
- Bottom right - evaluates leverage. Used to detect influential datapoints that will shift the gradient more than expected + also for outliers
null hypothesis: soil moisture has no effect on plant growth

5.5.4 Now the interpretation

Produce a sum of squares table:

anova(model_pgr)

## Analysis of Variance Table
## 
## Response: plant.growth.rate
##                       Df  Sum Sq Mean Sq F value    Pr(>F)    
## soil.moisture.content  1 2521.15 2521.15  156.08 < 2.2e-16 ***
## Residuals             48  775.35   16.15                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Output:
Large F value indicates that error variance is small relative to the variance attributed to the explanatory variable
- This leads to the tiny p value.
  - Both are good indications that the effect seen in the data isn’t the result of chance

Produce a summary table:

summary(model_pgr)

## 
## Call:
## lm(formula = plant.growth.rate ~ soil.moisture.content, data = plant_gr)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.9089 -3.0747  0.2261  2.6567  8.9406 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)             19.348      1.283   15.08   <2e-16 ***
## soil.moisture.content   12.750      1.021   12.49   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.019 on 48 degrees of freedom
## Multiple R-squared:  0.7648, Adjusted R-squared:  0.7599 
## F-statistic: 156.1 on 1 and 48 DF,  p-value: < 2.2e-16

produces table of estimates of the coefficients of the line that is the model
the slope that is associated with the explanatory variable (soil moisture) - the values of which are associated with the differences in plant growth rate

Superimpose linear model onto plot:

ggplot(plant_gr,
       aes(x=soil.moisture.content, y=plant.growth.rate)) +
  geom_point()+ 
  geom_smooth(method = 'lm') + #put a linear-model fitted line and the standard error of the fit using flash transparent gray onto graph 
  ylab("Plant Growth Rate (mm/week)") + 
  theme_bw()

## `geom_smooth()` using formula 'y ~ x'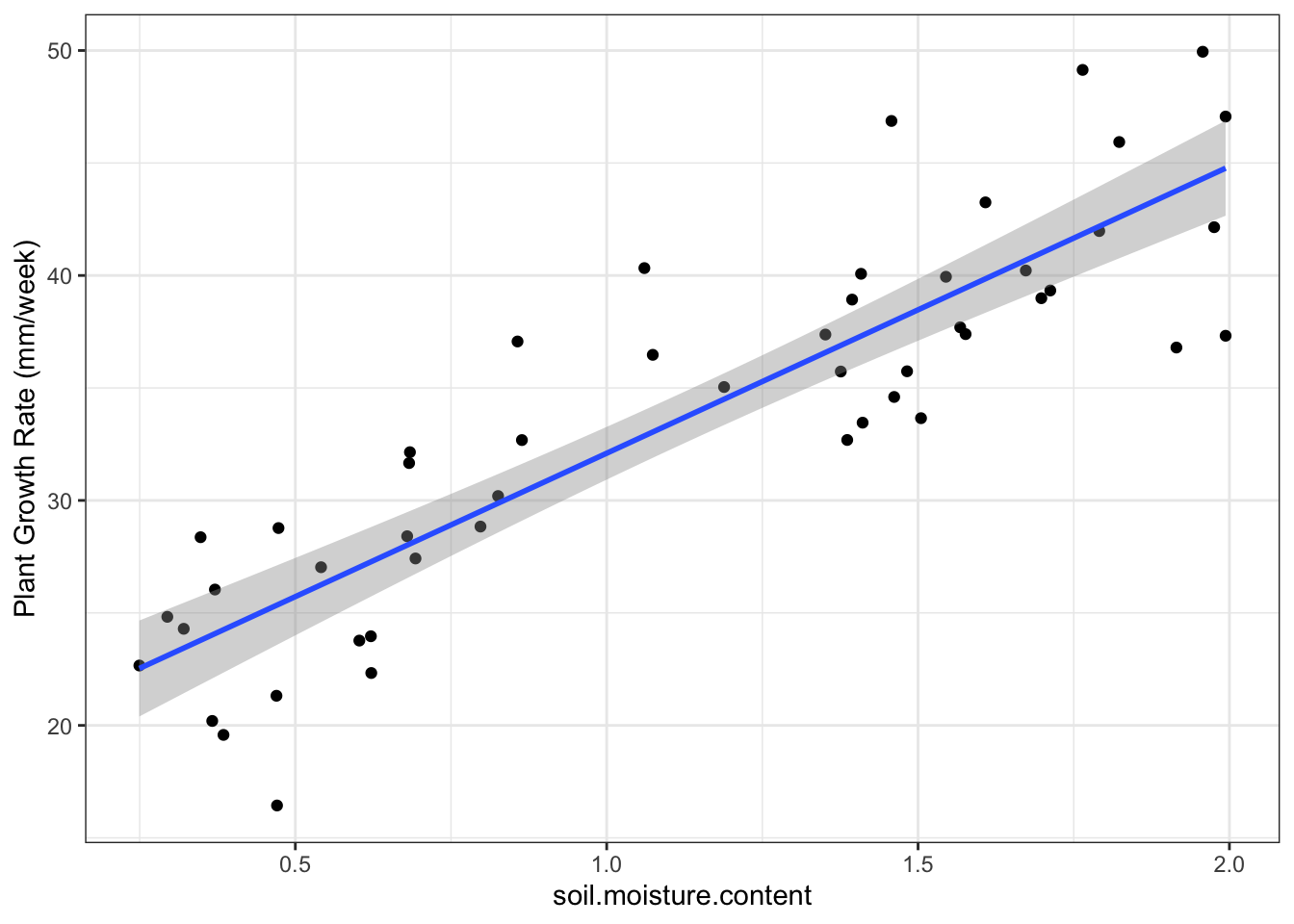

5.6 Analysis of variance: the one-way ANOVA

the one-way ANOVA is similiar to the previous example and the two-sample t-test with one key difference:
- the explanatory variable in the one-way ANOVA is a categorical variable (factor)
waterflea dataset - we ask:
- whether parasites alter waterflea growth rates
- whether each of three parasittes reduces growth rates relative to a control in which there was no parasite

urlfile05d="https://raw.githubusercontent.com/apicellap/data/main/Daphniagrowth.csv"
daphnia<-read.csv(url(urlfile05d))
glimpse(daphnia)

## Rows: 40
## Columns: 3
## $ parasite    <chr> "control", "control", "control", "control", "control", "co…
## $ rep         <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, …
## $ growth.rate <dbl> 1.0747092, 1.2659016, 1.3151563, 1.0757519, 1.1967619, 1.3…

Plot daphnia data:

ggplot(daphnia, aes(x = parasite, y=growth.rate)) + 
  geom_boxplot() +
  theme_bw() + 
  coord_flip() #flips the orientation of the graph 90˚ to the right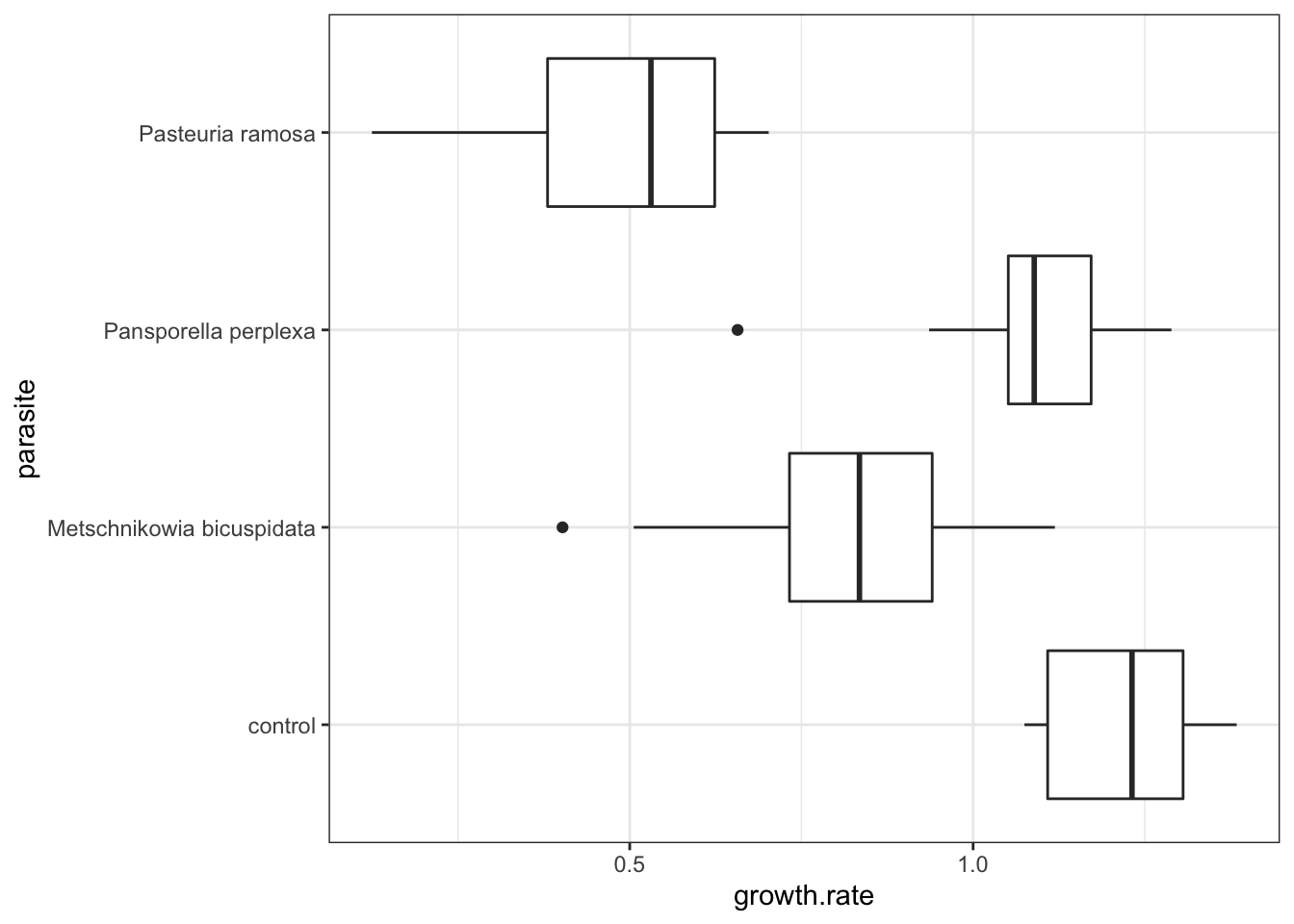

Visualization takeaways:
- There is substantial variation among the parasite groups
- The control group has the highest growth rate
- There is likely to be an overall effect of parasites on growth rate
- There may be an order in the impacts different parasites have on growth rates: P. ramosa < M. bicuspidata < P. perplexa

Create a model:

model_grow <- lm(growth.rate ~ parasite, data = daphnia)
model_grow

## 
## Call:
## lm(formula = growth.rate ~ parasite, data = daphnia)
## 
## Coefficients:
##                       (Intercept)  parasiteMetschnikowia bicuspidata  
##                            1.2139                            -0.4128  
##      parasitePansporella perplexa           parasitePasteuria ramosa  
##                           -0.1376                            -0.7317

Check the assumptions:

autoplot(model_grow, 
         smooth.colour = NA)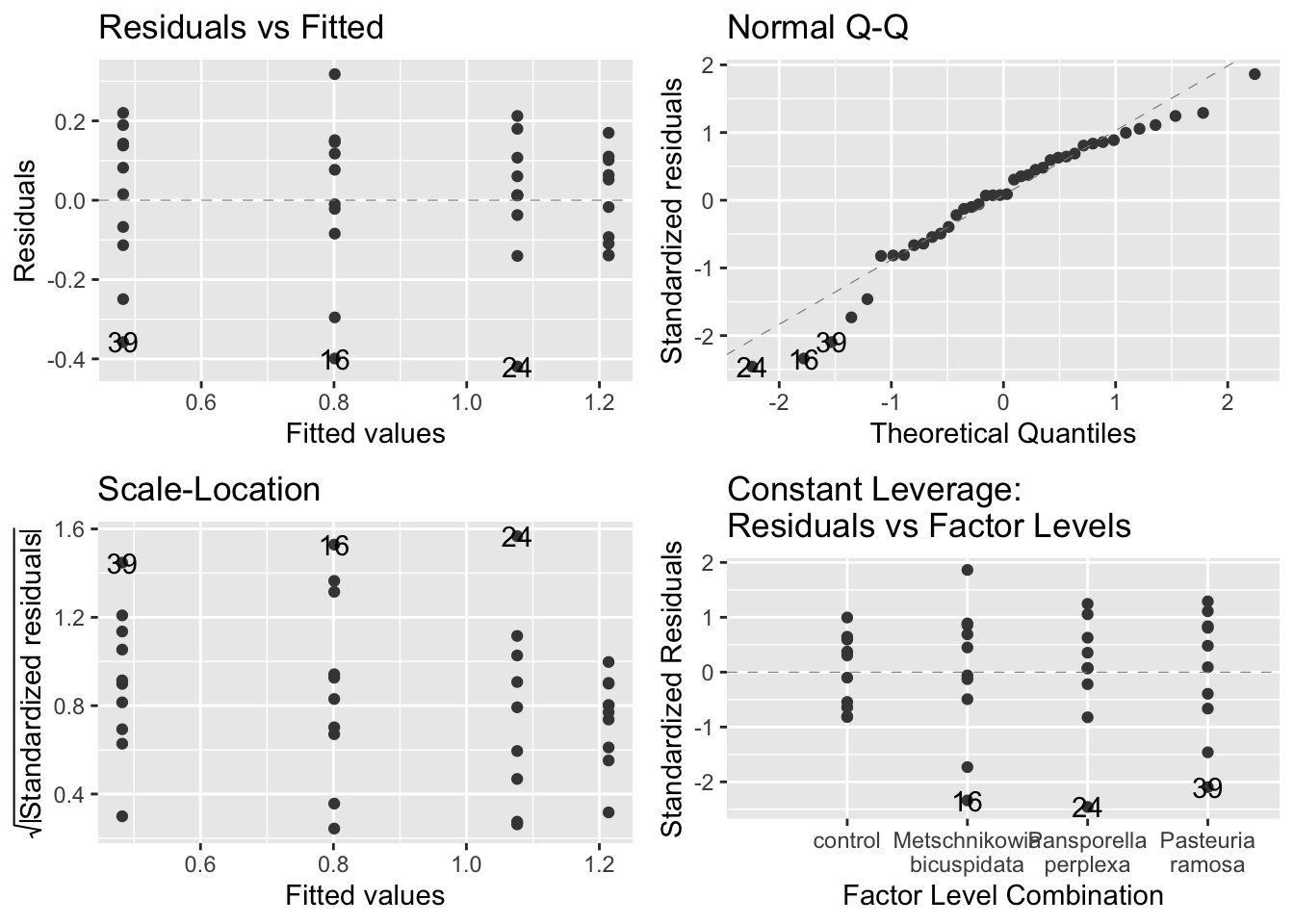

assumption-checking plots:
- The figures suggest that the assumptions are fine
- Even the upper right plot, the Q-Q plot, is within the bounds of expected variation

Produce anova table for model:

anova(model_grow)

## Analysis of Variance Table
## 
## Response: growth.rate
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## parasite   3 3.1379 1.04597  32.325 2.571e-10 ***
## Residuals 36 1.1649 0.03236                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

For a one-way anova, the null hypothesis is that all of the groups come from populations with (statistically) the same mean
- The F-value quantifies how likely this is to be true
  - F value is the ratio between the between group variation: within group variation
    - A large F value means that the between group variation is much larger

summary(model_grow)

## 
## Call:
## lm(formula = growth.rate ~ parasite, data = daphnia)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.41930 -0.09696  0.01408  0.12267  0.31790 
## 
## Coefficients:
##                                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                        1.21391    0.05688  21.340  < 2e-16 ***
## parasiteMetschnikowia bicuspidata -0.41275    0.08045  -5.131 1.01e-05 ***
## parasitePansporella perplexa      -0.13755    0.08045  -1.710   0.0959 .  
## parasitePasteuria ramosa          -0.73171    0.08045  -9.096 7.34e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1799 on 36 degrees of freedom
## Multiple R-squared:  0.7293, Adjusted R-squared:  0.7067 
## F-statistic: 32.33 on 3 and 36 DF,  p-value: 2.571e-10

Output:
table of coefficients:
- What is labelled as ‘(Intercept)’ is the control
- R tends to list things in alphabetical order
  - Of the levels of the explanatory variable, ‘control’ is the first alphabetically
  - In this context, we can assume that (Intercept) refers to the first level in alphabetical order - control - in this case
- Treatment contrasts report the differences between the reference level (the control in this case) and the other levels
  - So -0.41275 is the difference between the control level and the parasiteMetschnikowia bicuspidata level
  - In other words, the differences are the distances between the colored diamonds and the dotted black line in figure 6.1 below

Determine the means for each level:

sumDat <- daphnia %>% 
  group_by(parasite) %>%
  summarise(meanGR = mean(growth.rate))
sumDat

## # A tibble: 4 × 2
##   parasite                  meanGR
##   <chr>                      <dbl>
## 1 control                    1.21 
## 2 Metschnikowia bicuspidata  0.801
## 3 Pansporella perplexa       1.08 
## 4 Pasteuria ramosa           0.482

Manually determine the difference between control and other levels:

0.8011541   -1.2139088

## [1] -0.4127547

1.0763551 - 1.2139088

## [1] -0.1375537

0.4822030 - 1.2139088

## [1] -0.7317058

ggplot(daphnia, aes(x = parasite, y=growth.rate, color = parasite)) + 
  geom_point(size =2) + 
  geom_point(data = sumDat, aes( x = parasite, y = meanGR), shape = 18, size = 5) +
  geom_hline(yintercept = sumDat$meanGR[1],
             lwd=1,
             linetype = 'dotted',
             colour="black") + 
  geom_hline(yintercept = sumDat$meanGR[1],
             lwd=1,
             linetype = 'dotted',
             colour="black") + 
  xlab("")+
  theme_bw() + 
  coord_flip()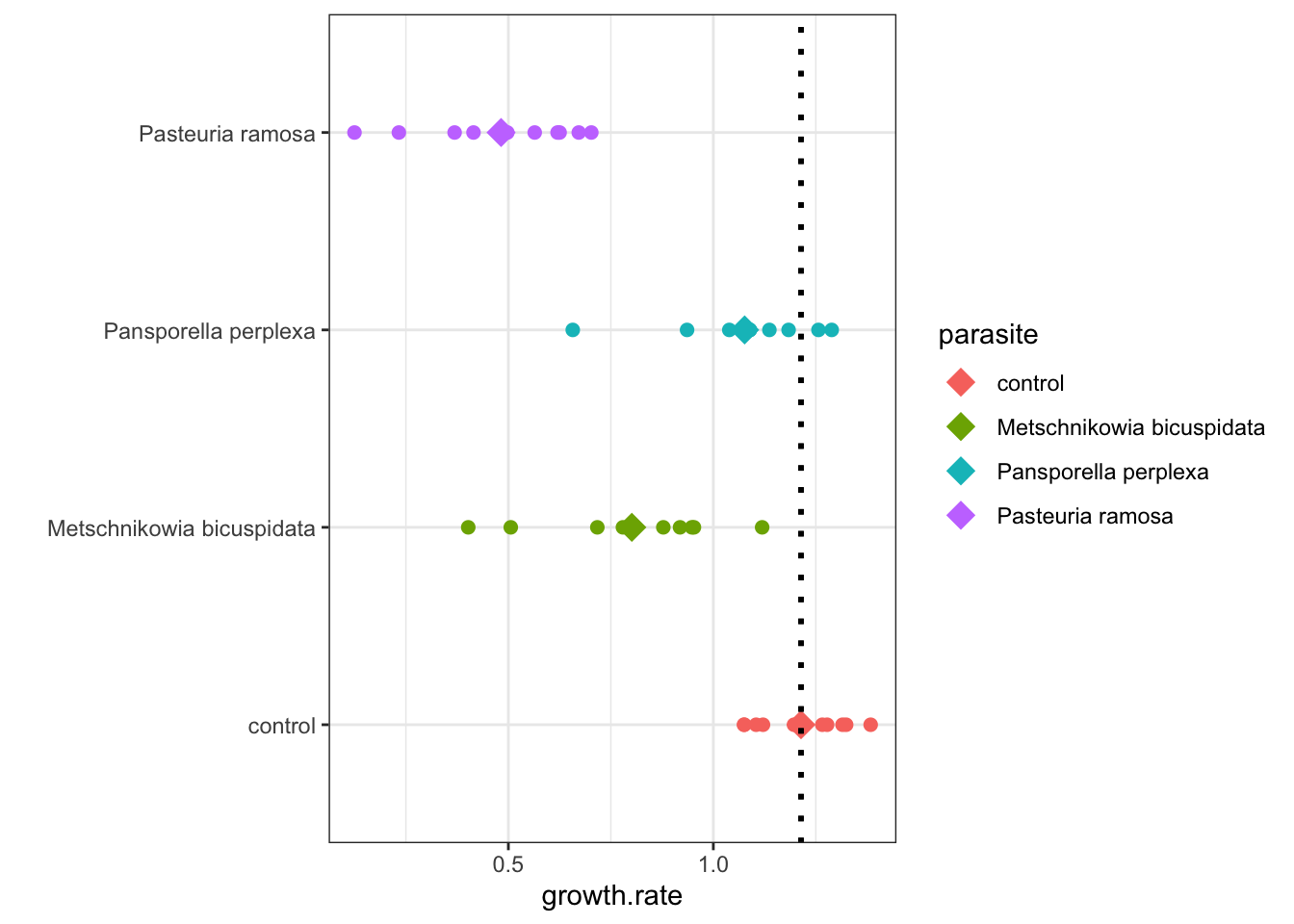

$\label{fig:figs}Daphnia Treatment Differences$

Figure 5.1: Daphnia Treatment Differences

4 Visualizing your data

6 Advancing Statistics in R

A Guide to Getting Started with R